「专题选做」博弈论题目选做 2

Sharti

「Codeforces 494E」Sharti

题目描述

$n \times n$ 的网格，给定 $m$ 个矩形，它们的并是白色的，剩下的格子是黑色的。两人博弈，每次可以选择一个边长不超过 $k$ 的正方形满足它的右下角是白色，然后反转这个正方形的颜色。不能操作者输，问先手是否必胜。

数据范围：$m \le 5 \times 10^4, k \le n \le 10^9$。

思路分析

介绍一个翻硬币的模型：给定一排硬币，每次选择一个右端点正面朝上的区间反转，不能操作者输。那么整个局面的 sg 值等于所有正面朝上的硬币单独存在时 sg 值的异或和。证明是考虑另一个问题：本来正面朝上的硬币处有棋子，每次选择一个右端点有棋子的区间然后拿掉右端点的一个棋子，并给其他点加上一个棋子。这两个问题是等价的，因为一个点有两个棋子时它们 sg 值为 $0$，就可以拿掉它们。

这个模型放到这个题里照样成立，所以我们考虑每个白格单独存在时的 sg 值。考虑打表：

1 1 1 1 1 1 1 1 | 1 1 1 1 1 1 1 1

发现 $k = 2, 3$ 时 sg 值都是左边的表，$k = 4, 5, 6, 7$ 时 sg 值都是右边的表。所以可以猜测表和不超过 $k$ 的最大 $2$ 的幂次有关。记 $b$ 表示满足 $2^x \le k$ 的最大 $x$，那么有：

$$\text{sg}(x, y) = 2^{\min\{\text{lowbit}(x), \text{lowbit}(y), b\}}$$

考虑对于每个 $2^i$ 分别计算。发现我们最后只要求矩形的面积并，考虑线段树维护两个值：$\text{cov(x)}, \text{ans(x)}$。每次区间 $\pm 1$ 时，我们找出区间对应的 $O(\log n)$ 个结点把它们的 $\text{cov}(x) \pm 1$。然后对于每个点，都有：

$$\text{ans}(x) = \begin{cases} \text{len}(x) & (\text{cov}(x) > 0) \\ 0 & (\text{cov}(x) = 0 \text{ and } x \text{ is leaf}) \\ \text{ans}(\text{lson(x)}) + \text{ans}(\text{rson(x)}) & (\text{otherwise}) \end {cases}$$

直接更新即可。时间复杂度 $O(n \log k \log n)$，具体细节见代码。

代码实现

#include <bits/stdc++.h>

银

「ZROI 967」银

思路分析

把游戏左右翻转，变成翻硬币模型，$\text{sg}(i) = 2^{\text{lowbit}(i)}$。设 $f(x)$ 表示 $x$ 的高位到低位的前缀异或和（例子：$f((100100)_2) = (111000)_2$），那么我们有 $f(0) = 0, f(a)\oplus f(b) = f(a \oplus b)$，以及 $\bigoplus_{i = 1}^{n}f(\text{sg}(i)) = n$。

设当前整个局面的 sg 值为 $X$，题目中合法的 $(l, r)$ 要满足：$\bigoplus_{i = l}^{r} \text{sg}(i) = X$。稍加转化得到 $\bigoplus_{i = l}^{r} f(\text{sg}(i)) = f(X)$，也就是 $(l - 1) \oplus r = f(X)$。发现对于一个 $r$ 存在对应的 $l - 1 < r$ 当且仅当 $f(X)$ 的最高位在 $r$ 的二进制下为 $1$，所以问题转化成了每次加一个数，删一个数，或查询某一位为 $1$ 的数的数量。维护 $f(X)$，直接模拟即可，时间复杂度 $O(n \log v)$。

代码实现

#include <bits/stdc++.h>

Tree-Tac-Toe

「Codeforces 1110G」Tree-Tac-Toe

题目描述

一棵 $n$ 个点的树，一开始一些点是白色。先手是白色，后手是黑色，每次一个人可以把一个没有颜色的点涂成自己的颜色。出现三个连续的同种颜色时持有该颜色的人就赢了，问最后是谁赢，或平局。

数据范围：$T \le 5 \times 10^4, \sum n \le 10^5$。

思路分析

首先我们可以去掉所有白点。考虑下图中的白点：

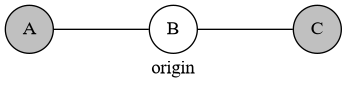
我们把它变成：

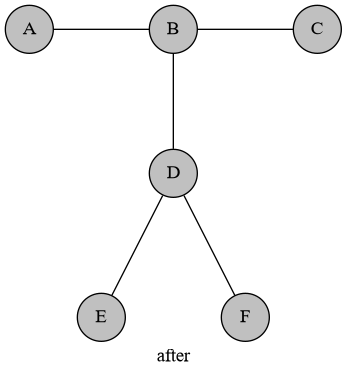
考虑这样的正确性。注意到 BDEF 这棵子树中谁都不可能赢，所以我们的最优策略是把 B 点变成自己的颜色。假设先手把 B 变成白色，那么如果后手不把 E 变成黑色，那么先手在下一步就能把 B 变成白色，然后他就赢了。也就是说第二步后手一定会把 E 变成黑色。那么剩下的两个点就和原图没有关系了，如果后手选了其中一个点先手把另一个点选掉即可。

接下来考虑没有白点的图。考虑下面两种情况：

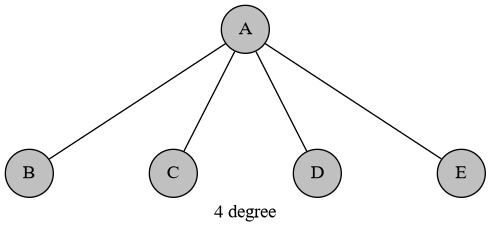
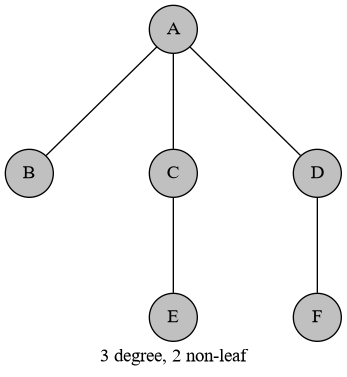
如果一个点度数为 $4$，或者它度数为 $3$ 且有至少两个非叶儿子，那么一定先手必胜。

考虑排出这些情况的图，图中每个点的度数都不超过 $3$，并且度数为 $3$ 的点最多只有 $2$ 个。考虑下面这种情况：

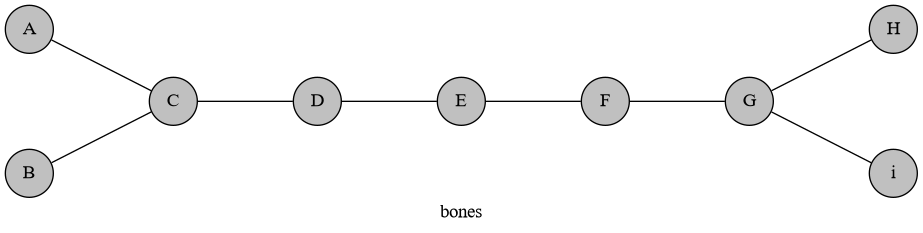
即两个度数为 $3$ 的点中间夹着奇数个点，其实它等价于下面的图：

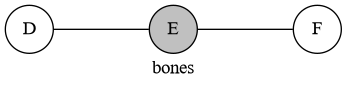
即两个白点之间夹着奇数个点。考虑这样的策略：每次选择左边白点向右的第二个点，这样黑点必须填在左边两个白点之间，然后问题就转化成了 $n’ = n - 2$ 的子问题。可以证明除了这种情况一定是平局，直接模拟，时间复杂度 $O(n)$。

代码实现

#include <bits/stdc++.h>

Chip Game

「Codeforces 1033G」Chip Game

题目描述

有 $n$ 堆石子，第 $i$ 堆有 $v_i$ 个。两人玩游戏，A 每轮从一堆中拿 $a$ 个石子，B 每轮从一堆中拿 $b$ 个石子，不能拿的人输。对于一种 $(a, b)$，共有四种情况：

• 不管谁先手都是 A 赢。（A 赢）
• 不管谁先手都是 B 赢。（B 赢）
• A 先手 A 赢，B 先手 B 赢。（先手赢）
• A 先手 B 赢，B 先手 A 赢。（后手赢）

问对于所有 $1 \le a, b \le m$，四种情况各有多少种。

数据范围：$n \le 100, m \le 10^5$。

思路分析

考虑特定 $(a, b)$ 的情况。首先把所有 $v_i$ 都对 $a + b$ 取模，容易证明这样是对的。不妨设 $a < b$，对于每一个 $v_i$ 讨论：

1. $0 \le v_i < a$，那么 $v_i$ 就谁都不能选。
2. $a \le v_i < b$，那么只有 A 能选一次，B 不能选。
3. $b \le v_i < 2a$，那么 A, B 都只能选一次。
4. $\max(2a, b) \le v_i < a + b$，那么 A 选完后 B 不能选，B 选完后谁都不能选。

那么我们扔掉 1，然后分类讨论：

• 若存在 2，那么 A 赢。
• 若不存在 2 且存在至少两个 4，那么 A 肯定可以抢到一个 4 把它变成 2，也就是 A 赢。
• 若不存在 2, 4，那么相当于先手后手抢 3，奇数个 3 先手赢，偶数个 3 后手赢。
• 若不存在 2 且只有一个 4，那么如果 A 先手他可以抢到 4，如果 B 先手他必须抢 4，然后变成全是 3 的情况。所以如果奇数个 3，那么 A 赢，否则先手赢。

这样就得到了一个 $O(nm^2)$ 的算法，不够快。考虑只计算先手、后手赢的情况数，其他两种情况可以用总数减去这些数来推出。枚举 $s = a + b$，首先不能有 2，也就是要满足 $a \ge \min(v_i + 1, s - v_i)$。其次 4 只有 $0, 1$ 个，也就是 $s - v_i \le a \le \lfloor \frac{v_i}{2} \rfloor$ 的 $v_i$ 只有不超过一个。同时我们也要记录 3 的个数，也就是 $a \ge \max(\lfloor \frac{v_i}{2} \rfloor + 1, s - v_i)$ 的个数。我们记录关键的端点，排完序扫一遍即可，时间复杂度 $O(m n \log n)$。

代码实现

#include <bits/stdc++.h>