「专题选做」简单计数题选做 1

SetAndSet

「Topcoder 12004」SetAndSet

题目描述

给 $n$ 个数 $a_1, a_2, \cdots, a_n$，要把它们划分成两个集合，使得两边的 And 一样，问方案数。

数据范围：$n \le 50, 0 \le a_i < 2^{20}$。

思路分析

也就是说对于每一位，如果存在一个数这一位为 $0$，那么这一位为 $0$ 的数不能全在同一边。考虑容斥，每次强制某些位让这一位为 $0$ 的数全在同一边。使用并查集维护即可，直接实现时间复杂度 $O(2^{20} \times 20n)$，容斥用 dfs 实现复杂度为 $O(2^{20} n)$，可以通过（忽略并查集复杂度）。

代码实现

#include <bits/stdc++.h>

Endless Spin

「HDU 4624」Endless Spin

题目描述

有 $n$ 个格子，每次随机选择一个区间染黑，问全染黑的期望时间。答案保留 $15$ 位小数。

数据范围：$T, n \le 50$。

思路分析

我们要求的是 $\max(T_1, T_2, \cdots, T_n)$，其中 $T_i$ 表示第 $i$ 个格子被覆盖的时间。考虑 Min-Max 容斥，计算 $\sum_{S \in [n]} (-1)^{\vert S \vert - 1} \min_{i \in S}(T_i)$。对于某个 $S$，我们要算出经过 $S$ 种某个点的区间个数 $x$，设总区间个数为 $y$，那么它对答案的贡献是容斥系数乘上 $\frac{y}{x}$。带上容斥系数套个 dp 即可，由于精度要求较高可以使用高精度 / int128，时间复杂度 $O(n^4)$。

代码实现

#include <bits/stdc++.h>

随机立方体

「CTS 2019」随机立方体（Luogu 5400）

题目描述

有 $n \times m \times l$ 的立方体，每个位置有 $[0, 1]$ 范围内随机的实数，一个数是极大的当且仅当它大于任何一个与它某一维坐标相同的数。问恰好有 $k$ 个极大的数的概率。

数据范围：$T \le 10, n, m, l \le 5 \times 10^6, k \le 100$。

思路分析

记 $N = \min(n, m, l)$，以及钦定 $i$ 个数极大，其他随便选的概率的和为 $A_i$，那么根据二项式反演，答案等于：

$$\text{Ans} = \sum_{i = k}^{N} \binom{i}{k} A_i (-1)^{i - k}$$

我们考虑 $A_i$ 怎么求。首先从小到大钦定 $i$ 个数，之后我们会得到一棵表示大小关系的树：

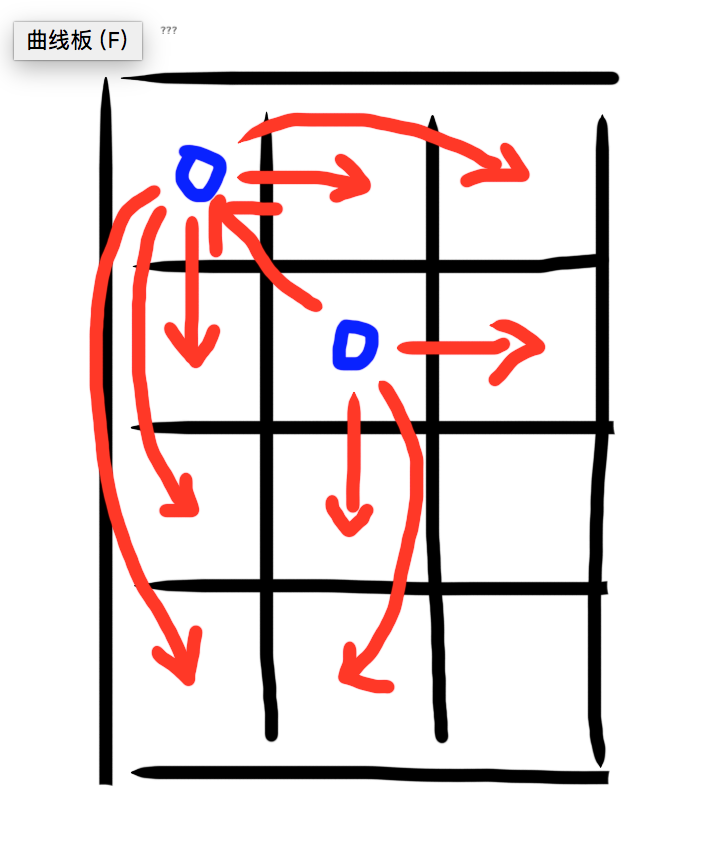
上图是二维时 $n = 4, m = 3, i = 2$ 的情况，两个极大值分别是 $(1, 1)$ 和 $(2, 2)$，一个格子指向另一个格子表示一个格子大于另一个格子。根据经典结论，概率应该是子树大小的倒数相乘，所以最终的式子是：

$$\begin {align*} & A_i = n^{\underline i} m^{\underline i} l^{\underline i} \prod_{j = 1}^{i} \frac{1}{nml - (n - j)(m - j)(l - j)} \\ & \text{Ans} = \sum_{i = k}^{N} \binom{i}{k} A_i (-1)^{i - k} \\ = & \sum_{i = k}^{N} \binom{i}{k} (-1)^{i - k} n^{\underline i} m^{\underline i} l^{\underline i} \prod_{j = 1}^{i} \frac{1}{nml - (n - j)(m - j)(l - j)} \end {align*}$$

直接计算即可，注意要用到线性求逆元，时间复杂度 $O(Tn)$。

代码实现

#include <bits/stdc++.h>

Square Constraints

「AGC 036F」Square Constraints

题目描述

求有多少个 $0, 1, \cdots, 2n - 1$ 的排列 $p$，满足 $n^2 \le i^2 + p_i^2 \le 4n^2$。

数据范围：$n \le 250$。

思路分析

考虑子问题：长度为 $0, 2, \cdots, m - 1$ 的排列 $p$ 有多少个满足 $p_i < a_i$。考虑先把 $a_i$ 从小到大排序，根据乘法原理，方案数就是 $\prod_{i = 0}^{m - 1} (a_i - i)$。

注意到这个做法是基于 $a_i$ 的大小排名的。考虑原题，发现限制的形状如下：

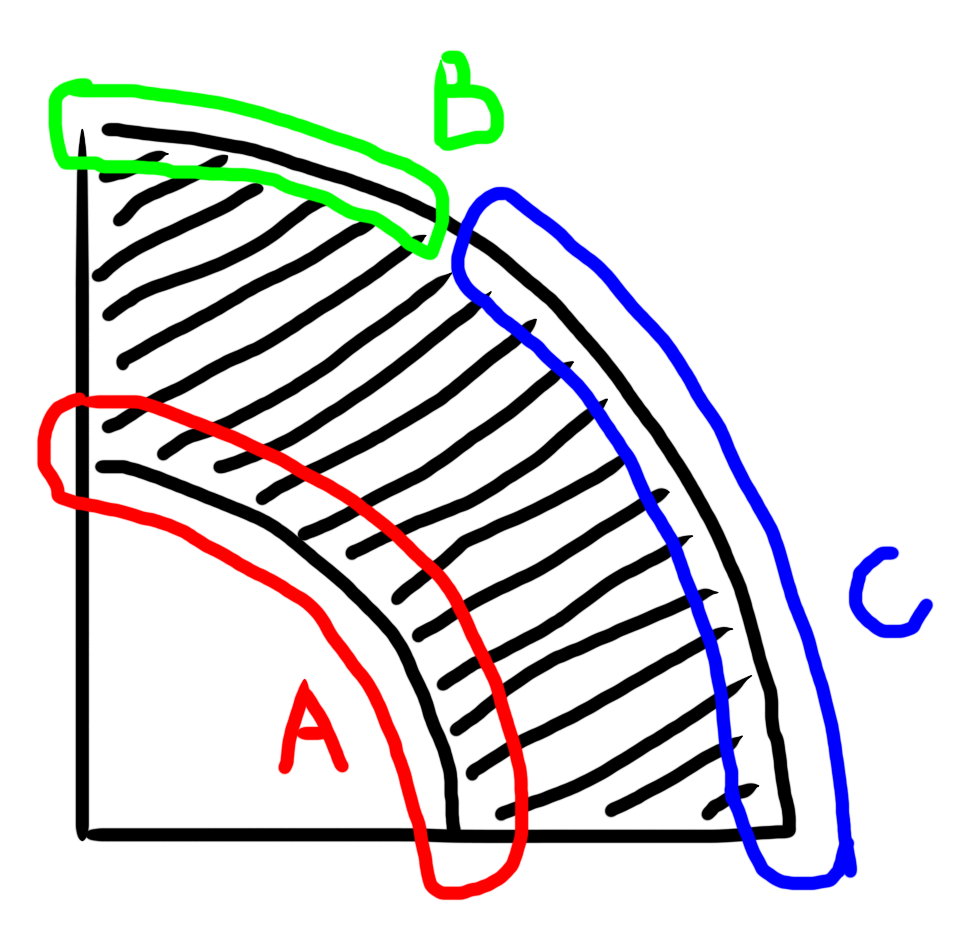
阴影部分是 $(i, p_i)$ 可以选的地方，空白部分是不能选的地方。我们考虑容斥，把前 $n$ 个限制拆成 $[p_i \le r_i] - [p_i \le l_i - 1]$。考虑把所有限制分成三类：A 类，B 类和 C 类。我们把所有限制按照高度从小到大排序，得到的序列一定长成这样：$\text{ACACAACACCBBBBB}$。在序列中，我们要选择所有的 C，以及第 $i$ 个 A 和第 $i$ 个 B 中的一个。额外地，每选到一个 A 后，系数就要乘上 $-1$。

考虑 dp 前 $2n$ 个字符，$f(i, j)$ 表示考虑前 $i$ 个字符，A 选了 $j$ 个的方案数。对于一个 A / C，我们容易计算它的排名，但是对于一个 A 对应的 B，我们就不能得到它的排名了。于是，我们考虑事先枚举要用 $k$ 个 A，然后再 dp，这样就可以得到 B 的排名。这样我们就得到了一个时间复杂度为 $O(n^3)$ 的做法。

代码实现

#include <bits/stdc++.h>

HamiltonianPaths

「Topcoder 14250」HamiltonianPaths

题目描述

给定一个 $n$ 个点的图，把它复制 $k$ 边，然后取补图，问新图的哈密尔顿路径条数，对 $998244353$ 取模。

数据范围：$n \le 14, k \le 5 \times 10^4$。

思路分析

也就是说限制整个完全图中不能经过 $km$ 条边。考虑容斥，枚举必须经过 $c$ 条边，那么对答案的贡献就是 $(-1)^c$ 乘上方案数。假设一个子图里经过了 $d$ 条不合法边，组成了 $e$ 条有向的链，那么将链定向后，对答案的贡献就是 $(-1)^d$，也就是说权值为 $(-1)^d$。最后如果缩点后还剩 $f$ 个点，方案数就是 $f!$。所以要算出每个图缩成 $g$ 个点的权值和，然后用 fft 求出大图缩成 $f$ 个点的权值和。一个子图的权值和可以通过简单状压 dp 实现，总时间复杂度 $O(2^n n^2 + 3^n n + kn \log kn)$。

代码实现

#include <bits/stdc++.h>

Fireflies

「HDU 6355」Fireflies

题目描述

给定 $n$ 个数 $p_1, p_2, \cdots, p_n$，令 $M = \lfloor \frac{\sum_{i = 1}^{n} (p_i + 1)}{2} \rfloor$，问有多少 $n$ 元组 $(x_1, x_2, \cdots, x_n)$ 满足：

• $1 \le x_i \le p_i$
• $\sum_{i = 1}^{n} x_i = M$

数据范围：$T \le 2000, n \le 32$，至多两组数据满足 $n > 24$。

思路分析

注意：此题中的 $\binom{n}{m}$ 定义为 $\frac{n^{\underline{m}}}{m!}$，所以 $n < 0$ 时的组合数也可以计算。

考虑容斥，$1 \le x_i \le p_i$ 的方案数为 $[x_i > 0] - [x_i > p_i]$。考虑将强制大于 $p_i$ 的数减去 $p_i$，然后使用插板法，问题就转化成了计算：

$$\sum_{S \in [n]} (-1)^{\vert S \vert} \binom{M - 1 - \sum_{i \in S} p_i}{n - 1} [M - 1 - \sum_{i \in S} p_i \ge 0]$$

直接计算不行，考虑折半搜索。使用范德蒙德恒等式：

$$\binom{a + b}{n} = \sum_{i = 0}^{n} \binom{a}{i} \binom{b}{n - i}$$

用到这题里就是：

$$\begin {align*} & (-1)^{\vert S \vert} \binom{M - 1 - \sum_{i \in S} p_i}{n - 1} [M - 1 - \sum_{i \in S} p_i \ge 0] \\ = & (-1)^{\vert L \vert + \vert R \vert} [M - 1 - \sum_{i \in S} p_i \ge 0] \times \sum_{i = 0}^{n - 1} \binom{M - 1 - \sum_{i \in L} p_i}{n - 1 - i} \binom{- \sum_{i \in R} p_i}{i} \end {align*}$$

那么我们左边、右边分别预处理组合数，然后 2 - pointers 合并即可。时间复杂度 $O(2^{\frac{n}{2}} n)$。

代码实现

#include <bits/stdc++.h>