Manju Game

记奇数格的和是 $A$，偶数格的和是 $B$。发现 $n$ 为偶数时，先手取 $\text{max}(A, B)$ 时后手总能保证自己有 $\min(A, B)$，直接输出答案即可。$n$ 为奇数时，先手取 $A$ 时后手总能保证自己有 $B$，问题在于先手取偶数格时该怎么办。考虑把先手的策略写成一棵二叉树，当到达一个状态先手决定取 $A$ 时它就是叶子结点，否则先手会选择一个偶数格，并把问题分成两个子问题（作为左右儿子），然后走左儿子还是右儿子是后手选择的。用二叉树的每个点把序列分段，先手的答案就是全部的 $B$ 加上某一段的 $A - B$，而这一段是后手决定的。问题转化成了把原序列去除若干个奇数格，分出来的所有段 $A - B$ 的最小值最大。二分答案，dp 求出是否存在一种方案每一段的和都 $\ge x$。暴力做是 $O(n^2)$ 的，但是发现只会从前缀和最小的点转移过来，就优化成 $O(n)$ 了。

1	#include <bits/stdc++.h>
2	using namespace std;
3
4	const int maxn = 3e5, inf = 3e8;
5	int n, a[maxn + 3], b[maxn + 3], w[maxn + 3], s[maxn + 3];
6	bool dp[maxn + 3];
7
8	bool check(int x) {
9	int mn = 0;
10	for (int i = 1; i <= n; i += 2) {
11	if (s[i] - mn >= x) {
12	dp[i] = true;
13	mn = min(mn, s[i + 1]);
14	} else {
15	dp[i] = false;
16	}
17	}
18	return dp[n];
19	}
20
21	int main() {
22	scanf("%d", &n);
23	for (int i = 1; i <= n; i++) {
24	scanf("%d", &a[i]);
25	b[i] = b[i - 1], w[i] = w[i - 1];
26	i & 1 ? b[i] += a[i] : w[i] += a[i];
27	}
28	for (int i = 1; i <= n; i++) {
29	s[i] = b[i] - w[i];
30	}
31	if (~n & 1) {
32	printf("%d %d\n", max(b[n], w[n]), min(b[n], w[n]));
33	} else {
34	int l = -inf, r = inf, mid;
35	while (l < r) {
36	mid = ((l + r + inf * 2 + 1) >> 1) - inf;
37	if (check(mid)) {
38	l = mid;
39	} else {
40	r = mid - 1;
41	}
42	}
43	int x = max(w[n] + l, b[n]);
44	printf("%d %d\n", x, b[n] + w[n] - x);
45	}
46	return 0;
47	}

Modulo Matrix

对于所有 $x + y$ 是偶数的格子根据 $x + y$ 分配一个素数，再根据 $x - y + 3n$ 分配一个素数（这样保证素数互不相同），然后该格子中最终的数就是两个素数乘起来。对于所有 $x + y$ 是奇数的格子分配所有相邻格子的最小公倍数 $+ 1$ 即可，注意特判 $n = 2$。时间复杂度 $O(n^2)$。

1	#include <bits/stdc++.h>
2	using namespace std;
3
4	typedef long long ll;
5	const int maxn = 500, dx[] = { 1, -1, 0, 0 }, dy[] = { 0, 0, 1, -1 };
6	int n, c[maxn + 3][maxn + 3], d[maxn + 3][maxn + 3], num[maxn << 2 \| 3];
7	ll a[maxn + 3][maxn + 3];
8	bool b[maxn + 3][maxn + 3];
9
10	ll gcd(ll a, ll b) {
11	return b ? gcd(b, a % b) : a;
12	}
13
14	ll lcm(ll a, ll b) {
15	if (!a \|\| !b) return a + b;
16	return a / gcd(a, b) * b;
17	}
18
19	int is_prime(int x) {
20	for (int i = 2; i * i <= x; i++) {
21	if (x % i == 0) return false;
22	}
23	return true;
24	}
25
26	bool valid(int x, int y) {
27	return x >= 1 && x <= n && y >= 1 && y <= n;
28	}
29
30	void work(int n) {
31	for (int i = 1; i <= n; i++) {
32	for (int j = 1; j <= n; j++) {
33	b[i][j] = ~(i + j) & 1;
34	}
35	}
36	int cur = 2;
37	for (int i = 1; i <= n; i++) {
38	for (int j = 1; j <= n; j++) {
39	if (b[i][j]) {
40	if (!num[i + j]) {
41	while (!is_prime(cur)) cur++;
42	num[i + j] = cur++;
43	}
44	c[i][j] = num[i + j];
45	}
46	}
47	}
48	for (int i = 1; i <= n; i++) {
49	for (int j = 1; j <= n; j++) {
50	if (b[i][j]) {
51	if (!num[i - j + n * 3]) {
52	while (!is_prime(cur)) cur++;
53	num[i - j + n * 3] = cur++;
54	}
55	d[i][j] = num[i - j + n * 3];
56	}
57	}
58	}
59	for (int i = 1; i <= n; i++) {
60	for (int j = 1; j <= n; j++) {
61	if (b[i][j]) {
62	a[i][j] = c[i][j] * d[i][j];
63	}
64	}
65	}
66	for (int i = 1; i <= n; i++) {
67	for (int j = 1; j <= n; j++) {
68	if (!b[i][j]) {
69	for (int k = 0; k < 4; k++) {
70	if (valid(i + dx[k], j + dy[k])) {
71	a[i][j] = lcm(a[i][j], a[i + dx[k]][j + dy[k]]);
72	}
73	}
74	a[i][j]++;
75	}
76	}
77	}
78	}
79
80	int main() {
81	scanf("%d", &n);
82	if (n == 2) {
83	puts("4 7");
84	puts("23 10");
85	return 0;
86	}
87	work(n);
88	for (int i = 1; i <= n; i++) {
89	for (int j = 1; j <= n; j++) {
90	printf("%lld%c", a[i][j], " \n"[j == n]);
91	}
92	}
93	return 0;
94	}

ABBreviate

将 $\text{a}$ 看成 $1$，$\text{b}$ 看成 $2$，一个字符串 $S$ 能缩成字符 $c$ 的条件是 $S$ 的和模 $3$ 同余于 $c$，并且 $\vert S \vert = 1$ 或者 $S$ 中存在两个相邻字符相同。首先，如果 $S = \text{ababab}\cdots$，那么答案为 $1$。对于其他 $S$，考虑它是否可以缩成串 $T$。对于 $T$ 的每一位，我们贪心的找到 $S$ 最短的一个前缀同余于 $T_i$，然后删去 $S$ 的那个前缀，最后会剩下一段 $S$ 的后缀，我们要求这段的和为 $0$。注意这是充要条件，如果最后一个串可以和剩余串合并，那么就并上去；否则最后一个串 + 剩余串一定是 $\text{a + bababa}\cdots$ 或者 $\text{b + ababab}\cdots$。我们找到之前的第一组两个相同的相邻位，然后把它向后合并剩余串长度次，这样就相当于把 $\text{ababab}\cdots$ 左移了剩余串长度次，就把剩余串消掉了。根据这个充要条件，我们就可以简单 dp 了，时间复杂度 $O(n)$。

1	#include <bits/stdc++.h>
2	using namespace std;
3
4	const int maxn = 1e5, mod = 1e9 + 7;
5	int n, a[maxn + 3], pos[maxn + 3][3], dp[maxn + 3], lst[maxn + 3];
6	char s[maxn + 3];
7
8	void upd(int &x, int y) {
9	x += y, x < mod ? 0 : x -= mod;
10	}
11
12	int main() {
13	scanf("%s", s + 1);
14	n = strlen(s + 1);
15	bool flag = true;
16	for (int i = 1; i < n; i++) {
17	flag &= s[i] != s[i + 1];
18	}
19	if (flag) {
20	puts("1");
21	return 0;
22	}
23	for (int i = 1; i <= n; i++) {
24	a[i] = s[i] == 'a' ? 1 : 2;
25	a[i] = (a[i] + a[i - 1]) % 3;
26	}
27	for (int i = n; i; i--) {
28	lst[a[i]] = i;
29	for (int j = 1; j <= 2; j++) {
30	pos[i][j] = lst[(a[i - 1] + j) % 3];
31	}
32	}
33	dp[0] = 1;
34	for (int i = 0; i < n; i++) {
35	for (int j = 1; j <= 2; j++) {
36	if (pos[i + 1][j]) {
37	upd(dp[pos[i + 1][j]], dp[i]);
38	}
39	}
40	}
41	int ans = 0;
42	for (int i = 1; i <= n; i++) {
43	if ((a[n] - a[i] + 3) % 3 == 0) {
44	upd(ans, dp[i]);
45	}
46	}
47	printf("%d\n", ans);
48	return 0;
49	}

Grafting

首先枚举一个点假设它不会动，把它作为根，求出两个树的交。两棵树在交中的点不用动，A 树中其他的点都要动到 B 树中其他的点处。对于 A 树中的一对都要动的父子，儿子肯定比父亲先动；对于 B 树中的一对都要加入的父子，父亲肯定比儿子先加上。判断先后关系是否有环即可。可是有一种特殊情况，就是所有点都会动：

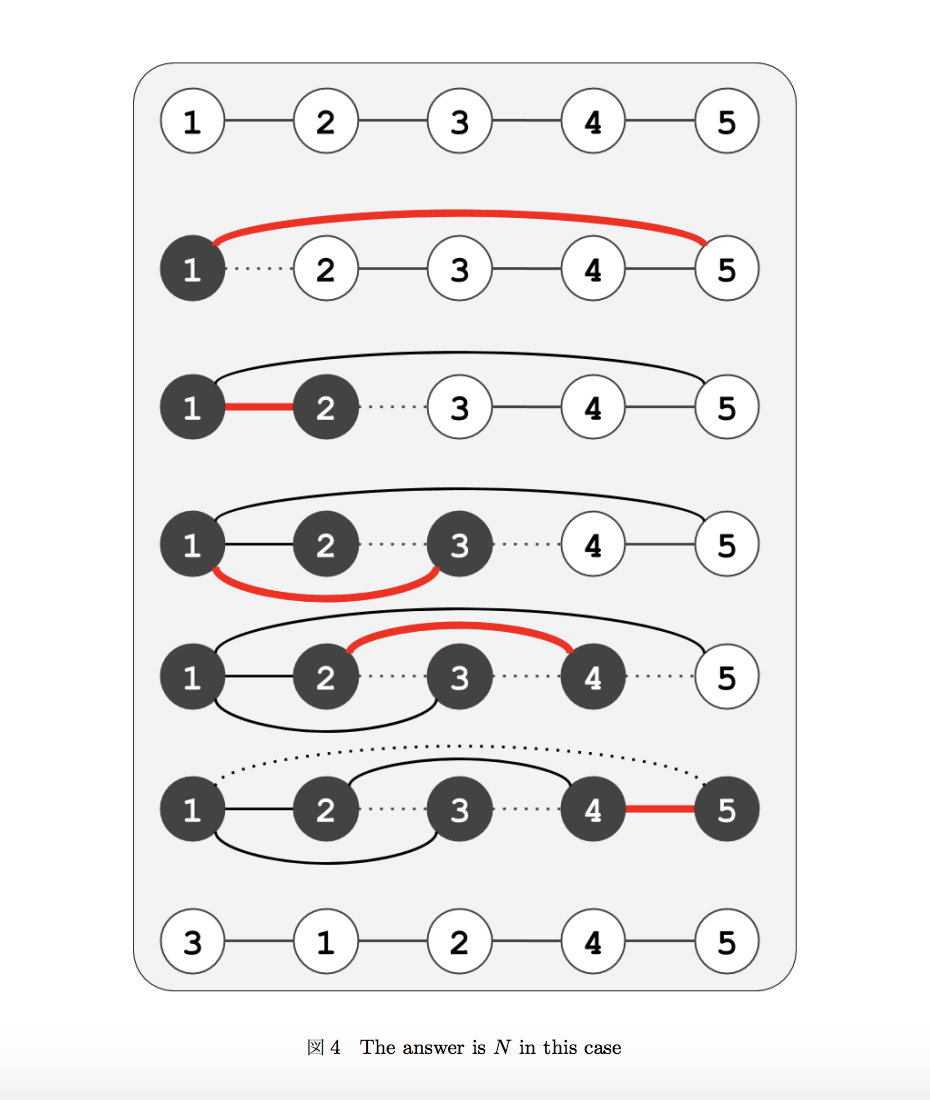
上图中是一个例子。于是我们还要枚举第一次移动了哪个叶子，移动到了哪里。之后这个叶子就不会动了，我们钦定这个叶子为根即可。时间复杂度 $O(n^3)$。

1	#include <bits/stdc++.h>
2	#define clear(x) memset(x, 0, sizeof(x))
3	using namespace std;
4
5	const int maxn = 50;
6	int T, n, a[maxn + 3][maxn + 3], b[maxn + 3][maxn + 3], c[maxn + 3], d[maxn + 3], deg[maxn + 3];
7	bool vis[maxn + 3];
8	vector<int> G[maxn + 3];
9
10	void add(int u, int v) {
11	G[u].push_back(v), deg[v]++;
12	}
13
14	void dfs(int u) {
15	vis[u] = true;
16	for (int v = 1; v <= n; v++) {
17	if (a[u][v] && b[u][v] && !vis[v]) {
18	dfs(v);
19	}
20	}
21	}
22
23	void dfs_1(int u, int pa = 0) {
24	for (int v = 1; v <= n; v++) {
25	if (a[u][v] && v != pa) {
26	if (!vis[u]) {
27	add(v, u);
28	}
29	dfs_1(v, u);
30	}
31	}
32	}
33
34	void dfs_2(int u, int pa = 0) {
35	for (int v = 1; v <= n; v++) {
36	if (b[u][v] && v != pa) {
37	if (!vis[u]) {
38	add(u, v);
39	}
40	dfs_2(v, u);
41	}
42	}
43	}
44
45	bool check() {
46	queue<int> Q;
47	int cnt = 0;
48	for (int i = 1; i <= n; i++) {
49	if (!deg[i]) {
50	Q.push(i);
51	}
52	}
53	while (!Q.empty()) {
54	int u = Q.front();
55	Q.pop(), cnt++;
56	for (int i = 0, v; i < G[u].size(); i++) {
57	v = G[u][i];
58	if (!--deg[v]) {
59	Q.push(v);
60	}
61	}
62	}
63	return cnt == n;
64	}
65
66	int solve(int u) {
67	clear(vis);
68	dfs(u);
69	for (int i = 1; i <= n; i++) {
70	vector<int>().swap(G[i]);
71	}
72	clear(deg);
73	dfs_1(u);
74	dfs_2(u);
75	if (!check()) {
76	return -1;
77	}
78	int cnt = 0;
79	for (int i = 1; i <= n; i++) {
80	cnt += vis[i];
81	}
82	return cnt;
83	}
84
85	int main() {
86	scanf("%d", &T);
87	while (T --> 0) {
88	scanf("%d", &n);
89	clear(a), clear(b), clear(c), clear(d);
90	for (int i = 1, u, v; i < n; i++) {
91	scanf("%d %d", &u, &v);
92	a[u][v] = a[v][u] = 1;
93	c[u]++, c[v]++;
94	}
95	for (int i = 1, u, v; i < n; i++) {
96	scanf("%d %d", &u, &v);
97	b[u][v] = b[v][u] = 1;
98	d[u]++, d[v]++;
99	}
100	int ans = -1;
101	for (int i = 1; i <= n; i++) {
102	ans = max(ans, solve(i));
103	}
104	for (int i = 1; i <= n; i++) if (c[i] == 1) {
105	for (int j = 1; j <= n; j++) if (a[i][j]) {
106	a[i][j] = a[j][i] = 0;
107	for (int k = 1; k <= n; k++) if (k != i && k != j) {
108	a[i][k] = a[k][i] = 1;
109	ans = max(ans, solve(i) - 1);
110	a[i][k] = a[k][i] = 0;
111	}
112	a[i][j] = a[j][i] = 1;
113	}
114	}
115	printf("%d\n", ans == -1 ? -1 : n - ans);
116	}
117	return 0;
118	}

Min Cost Cycle

首先我们可以把 min 看作随便选择 $A_i, B_j$ 中的一个。对于一个环的方案，我们把对答案贡献为 $A_ix + B_iy$ 的点称为 $(x, y)$。如果不存在 $(0, 0)$，那么只能是全部 $(0, 1)$ 或全部 $(1, 0)$；如果存在 $(0, 0)$，肯定存在相同数量的 $(1, 1)$，可以构造方案：

$(0, 0), (1, 1), (0, 0), \cdots, (1, 1), (0, 0), (1, 0), (1, 0), \cdots, (1, 0), (1, 1), (0, 1), (0, 1) \cdots, (0, 1)$

那么我们枚举 $i$，钦定 $i$ 是 $(1, 1)$，剩下的点从其他的所有数里选 $n - 2$ 个最小的出来即可。时间复杂度 $O(n \log n)$。

1	#include <bits/stdc++.h>
2	using namespace std;
3
4	typedef long long ll;
5	const int maxn = 2e5;
6	int n, m, a[maxn + 3], b[maxn + 3], p[maxn + 3][3];
7	ll sum[maxn + 3];
8
9	struct node {
10	int id, type, val;
11	friend bool operator < (const node &a, const node &b) {
12	return a.val < b.val;
13	}
14	} x[maxn + 3];
15
16	int main() {
17	scanf("%d", &n);
18	for (int i = 1; i <= n; i++) {
19	scanf("%d %d", &a[i], &b[i]);
20	x[++m].id = i, x[m].type = 1, x[m].val = a[i];
21	x[++m].id = i, x[m].type = 2, x[m].val = b[i];
22	}
23	ll A = 0, B = 0;
24	for (int i = 1; i <= n; i++) {
25	A += a[i], B += b[i];
26	}
27	ll ans = min(A, B);
28	sort(x + 1, x + m + 1);
29	for (int i = 1; i <= m; i++) {
30	p[x[i].id][x[i].type] = i;
31	sum[i] = sum[i - 1] + x[i].val;
32	}
33	for (int i = 1; i <= n; i++) {
34	int l = p[i][1], r = p[i][2];
35	if (l > r) {
36	swap(l, r);
37	}
38	if (l - 1 >= n - 2) {
39	ans = min(ans, sum[n - 2] + x[l].val + x[r].val);
40	} else if (r - 2 >= n - 2) {
41	ans = min(ans, sum[n - 1] + x[r].val);
42	} else {
43	ans = min(ans, sum[n]);
44	}
45	}
46	printf("%lld\n", ans);
47	return 0;
48	}

Chords

先考虑计算 $n$ 个点随便连的方案数 $g(n)$，发现 $g(2n - 1) = 0$，$g(2n) = (2n - 1)!!$。令 $f(i, j)$ 表示一个联通块点编号最小值为 $i$ 最大值为 $j$ 的方案数，那么有：

$f(i, j) = g(c(i, j)) - \sum_{k = i + 1}^{j - 1} f(i, k) \times g(c(k + 1, j))$

$c(i, j)$ 表示 $[i, j]$ 中有多少点没被选。值得注意的是如果一个区间满足有一段弧一端在区间内部，另一端在区间外部，$f(i, j)$ 必须等于 $0$。计算答案时直接把每个 $f(i, j)$ 乘上 $g(2(n - k) - c(i, j))$ 累加即可。时间复杂度 $O(n^3)$。

1	#include <bits/stdc++.h>
2	using namespace std;
3
4	const int maxn = 600, mod = 1e9 + 7;
5	int n, k, a[maxn + 3], b[maxn + 3], g[maxn + 3];
6	int dp[maxn + 3][maxn + 3], cnt[maxn + 3][maxn + 3];
7	bool val[maxn + 3][maxn + 3];
8
9	bool in(int x, int l, int r) {
10	return x >= l && x <= r;
11	}
12
13	int main() {
14	scanf("%d %d", &n, &k);
15	for (int i = 1; i <= k; i++) {
16	scanf("%d %d", &a[i], &b[i]);
17	}
18	g[0] = 1;
19	for (int i = 1; i <= n * 2; i++) {
20	g[i] = i & 1 ? 0 : 1ll * g[i - 2] * (i - 1) % mod;
21	}
22	for (int i = 1; i <= n * 2; i++) {
23	for (int j = i + 1; j <= n * 2; j++) {
24	val[i][j] = true;
25	for (int t = 1; t <= k; t++) {
26	if (in(a[t], i, j) ^ in(b[t], i, j)) {
27	val[i][j] = false;
28	break;
29	}
30	}
31	if (val[i][j]) {
32	for (int t = 1; t <= k; t++) {
33	cnt[i][j] += in(a[t], i, j) + in(b[t], i, j);
34	}
35	}
36	}
37	}
38	int ans = 0;
39	for (int d = 2; d <= n * 2; d += 2) {
40	for (int i = 1, j = d; j <= n * 2; i++, j++) {
41	if (!val[i][j]) continue;
42	dp[i][j] = g[d - cnt[i][j]];
43	for (int k = i + 1; k < j; k++) {
44	dp[i][j] = (dp[i][j] + 1ll * (mod - dp[i][k]) * g[j - k - cnt[k + 1][j]]) % mod;
45	}
46	ans = (ans + 1ll * dp[i][j] * g[(n - k) * 2 - (d - cnt[i][j])]) % mod;
47	}
48	}
49	printf("%d\n", ans);
50	return 0;
51	}

「集训队作业」IOI 2020 集训队作业小结 3

目录