「集训队作业」IOI 2020 集训队作业小结 1

简介

本文包括 IOI 2020 集训队作业第 7 到 12 题的题解。

• 「AGC 022E」 Median Replace
• 「AGC 022F」 Checkers
• 「AGC 023D」 Go Home
• 「AGC 023F」 01 on Tree
• 「AGC 024D」 Isomorphism Freak
• 「AGC 024E」 Sequence Growing Hard

Median Replace

「AGC 022E」Median Replace

题目描述

对于一个 01 串，每次选三个连续的数字删除后插入它们的中位数，如果存在一种方案操作多次后变成只有 1 的串，那么称这个串是好的。给定长度为 $n$ 的串（$n$ 是奇数），其中的一些字符是问号，问有多少种将问号替换为 0, 1 的方案，使得得到的 01 串是好的。

数据范围：$n \le 3 \times 10^5$。

思路分析

考虑建出自动机：

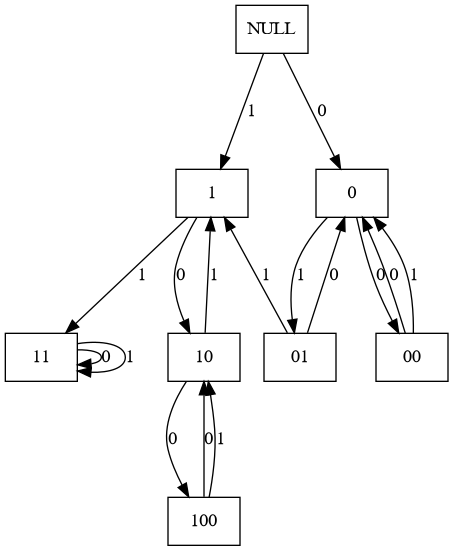
其中 1 和 11 为终止态。我们直接在上面 dp 算出走 $n$ 步到终止态的方案数即可，时间复杂度 $O(n)$。

代码实现

#include <bits/stdc++.h>

Checkers

「AGC 022F」Checkers

题目描述

有 $n$ 个棋子在数轴上，第 $i$ 个的 x 坐标为 $X^i$（$X$ 为一个足够大的数）。进行 $n - 1$ 次操作，每次选择两个棋子 $A, B$，让 $A$ 的 x 坐标变为 $A$ 关于 $B$ 的对称点，然后删除 $B$。最后会留下一个棋子，问它有多少种可能的坐标。

数据范围：$n \le 50$。

思路分析

我们将 $A$ 跳过 $B$ 的操作看作树上 $A$ 成为了 $B$ 的父亲，这样操作序列就可以看成一棵树。不难发现深度为 $d$ 的点对答案的贡献为 $\pm 2^d$，我们只要考虑它的正负号。考虑最终操作树上的某个点，在它的某个儿子合并到它的时候，以及它的所有祖先在它之后加入儿子的时候，它的符号都会被取反。实际上，我们不用考虑所有祖先，只用考虑自己的父亲，因为祖先可以通过父亲做前缀和来得到。

对于某一个父亲，如果它有 $k$ 个儿子，那么就有 $\lfloor\frac{k}{2}\rfloor$ 个儿子之后加入的兄弟数量是奇数。我们考虑一层一层地 dp：$dp(i, j)$ 表示用了 $i$ 个点，在最后一层中有 $j$ 个点的儿子数应该是奇数（预支了 $j$ 个点有奇数个儿子）的方案数。考虑枚举下一层有 $k$ 个点，那么就有 $\frac{k - j}{2}$ 个点的父亲在它以后加入了奇数个点。注意这时我们还没有考虑下一层的儿子结点。

接下来我们枚举实际上有 $x$ 个结点的贡献是负的（考虑儿子）。那么，如果 $x \ge \frac{k - j}{2}$，我们就让要 $x - \frac{k - j}{2}$ 个原本贡献是正的点取反；否则 $x < \frac{k - j}{2}$，我们就要让 $\frac{k - j}{2}$ 个原本贡献是负的点取反。而取反的方法就是给该点预支奇数个儿子，所以我们会从 $dp(i, j)$ 转移到 $dp(i + k, \vert x - \frac{k - j}{2} \vert)$，不同的正负贡献的值的数量是 $C_{n - i}^k \times C_k^x$。直接 dp 即可，时间复杂度 $O(n^4)$。

代码实现

#include <bits/stdc++.h>

Go Home

「AGC 023D」Go Home

题目描述

有 $n$ 个公寓，第 $i$ 个坐标为 $X_i$，人数为 $P_i$。公司在 $S$，下班后所有人都乘坐大巴回家。大巴一到家门口人就会下车，每个时刻大巴上的人会投票（向左或向右），然后大巴往票数多的一方开一格。每个人都要最小化回自己家的时间，问最后一个人回家的时间。

数据范围：$n \le 10^5$。

思路分析

首先，如果 $S$ 在第一栋楼左边或者第 $n$ 栋楼右边，它肯定是顺序经过所有楼。否则，我们看它是先经过 $1$ 号楼还是 $n$ 号楼。如果 $P_1 \ge P_n$，在车到达第 $n - 1$ 栋楼时，想向右的人就只有 $n$ 号楼里的人了，其他人都想向左，而 $P_1 \ge P_n$，所以车肯定会向左开，一直开到 $1$。也就是说，$P_1 \ge P_n$ 时，车会先到达 $1$ 号楼后到达 $n$ 号楼。这时，$n$ 号楼的人就会先让车向左，因为这样可以缩短他们回家的时间。这样，我们就可以将 $P_1 \gets P_1 + P_n$，并删掉 $n$ 号楼。$P_1 < P_n$ 时同理，这样我们就可以把问题转化成规模更小的问题，所以直接递归即可。时间复杂度 $O(n)$。

代码实现

#include <bits/stdc++.h>

01 on Tree

「AGC 023F」01 on Tree

题目描述

给定 $n$ 个点的树，第 $i$ 个点上的数是 $v_i \in {0, 1}$。每个父亲向儿子连一条边，求点的一个拓扑序，使得构成的 01 序列逆序对数最小。

数据范围：$n \le 2 \times 10^5$。

思路分析

典型的一种树上贪心套路。假设一开始每个点都是一个独立的集合，每次我们选择一个最优的集合将它与它的父亲合并，并同时计算对答案的贡献。在这题中，最优的集合就是 $\frac{C_0}{C_1}$ 最大的集合，其中 $C_k$ 表示 $k$ 的个数。证明过程是考虑某个点的两个儿子交换合并顺序后答案会不会变得更优，这里省略。用堆加并查集维护即可，时间复杂度 $O(n \log n)$。

代码实现

#include <bits/stdc++.h>

Isomorphism Freak

「AGC 024D」Isomorphism Freak

题目描述

定义一棵点有颜色的树是好的当且仅当对于任意两个颜色相同的结点，这棵树以它们为根形成的两棵有根树同构。给定 $n$ 个点的树，要加上若干个点，并给点染上颜色，使得树是好的。问最小的颜色数量，以及在颜色数量最小的情况下树上叶子结点个数的最小值。

数据范围：$n \le 100$。

思路分析

发现第一问答案为 $\lceil \frac{d}{2} \rceil$，其中 $d$ 表示直径长度（点数）。第二问分类讨论：如果 $d$ 是偶数，那么直径中心所在的边分出的两个子树中，每个深度相同的点儿子数量都要相同。如果 $d$ 是奇数，那么直径中心是点，会分出多棵子树，其中的每个深度相同的点儿子数量也要相同；或者我们也有可能在直径下面再加一个点，转化为 $d$ 是偶数的情况。由于 $n$ 很小，直接暴力即可，时间复杂度 $O(n^3)$。

代码实现

#include <bits/stdc++.h>

Sequence Growing Hard

「AGC 024E」Sequence Growing Hard

题目描述

求这样的 $(A_0, A_1, \cdots, A_n)$ 组数：

• $A_i$ 是长度为 $i$ 的序列，每个元素都是 $[1, k]$ 中的整数。
• $A_{i + 1}$ 是 $A_i$ 插入一个元素得到的。
• $A_{i + 1}$ 的字典序大于 $A_i$。

数据范围：$n, k \le 300$。

思路分析

考虑插入什么数会使字典序变大。假设我们要在数 $y$ 之前插入 $x$，那么要么 $x > y$，要么 $x = y$ 并且 $x$ 比 $y$ 后面第一个不等于 $y$ 的数大。考虑第二种情况得到的序列，其实和在第一个不等于 $y$ 的数之前插入 $x$ 没有区别，所以问题转化成了只有第一种情况。对于序列中的每个数，可以看作一个二元组 $(p_i, v_i)$ 分别表示它是第几次插入的，以及它的权值。在 $A_0$ 中我们建立一个虚拟的二元组 $(0, 0)$，这样之后每一次的插入我们都可以看作在某个二元组 $(x, y)$ 之前插入 $(i, v_i)$，满足 $y > v_i$。我们将在某个二元组之前插入二元组看作将新的二元组作为之前二元组的一个孩子，这样问题就转化成了一个有根树计数问题，每个结点是一个二元组，并满足：

• 根结点的二元组是 $(0, 0)$。
• 二元组的第一维形成排列，第二维的数在 $[0, k]$ 中。
• 二元组的父亲的两维小于儿子的两维。

设 $f(i, j)$ 表示 $i$ 个点的树，根结点的第二维是 $j$ 的方案数。我们考虑将 $i$ 个节点的第一维根据相对顺序用 $0, 1, \cdots, i - 1$ 来编号，观察到 $1$ 的父亲肯定是 $0$，所以我们枚举 $1$ 号结点子树的大小 $s$ 以及第二维的值 $l$，就可以列出转移方程：

$$f(i, j) = \sum_{s = 1}^{i - 1} \sum_{l = j + 1}^{k} f(s, l) \times f(i - s, j) \times C_{i - 2}^{s - 1}$$

答案就是 $f(n + 1, 0)$。前缀和优化即可，时间复杂度 $O(n^3)$。

代码实现

#include <bits/stdc++.h>