「NOI 2018」情报中心（线段树 + 虚树）

题目描述

「NOI 2018」情报中心（LOJ 2722）

给定一棵 $n$ 个点的树，第 $i$ 条边有权值 $c_i$。有 $m$ 条路径，第 $i$ 条路径有权值 $v_i$。求从 $m$ 条路径中选出两条至少有一条边相交的路径，得到的 $链并上的边权和 − 两条链的总费用$ 的最大值​。

数据范围：$\sum{n} \le 10^6, \sum {m} \le 2 \times 10^6, 0 \le c_i \le 10^9, 0 \le v_i \le 10^{10} \times n$。

提示：分两条路径的 LCA 相同或不同讨论。

思路分析

第一部分

发现如果两条路径的 LCA 不同，那么它们的交一定是直上直下的一段。

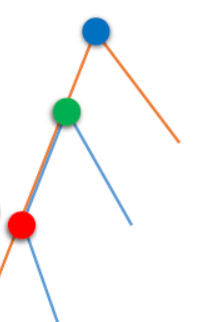
如上图所示，我们考虑红色和蓝色两条路径。这两条路径形成的权值为：$两条链的总长度 - 两条链的总费用 - (红点到根的距离 - 绿点到根的距离)$。

我们考虑枚举红点，并同时维护经过红点的所有路径。具体地，我们对每个点 $x$ 维护 $f(x, y)$ 表示所有经过点 $x$ 的、LCA 为 $y$ 的路径中，$长度 - 费用$ 的最大值。这样，我们求出 $f(x)$ 后，就可以用 $\max_{i, j}\lbrace f(x, i) + f(x, j) + \max\lbrace d(i), d(j)\rbrace \rbrace - d(x)$ 更新答案，其中 $d(x)$ 表示点 $x$ 到根的距离。当然，我们发现答案要求的是最大值，所以上式就可以简化为：$\max_{i, j}\lbrace f(x, i) + f(x, j) + d(i)\rbrace - d(x)$。

我们考虑使用下标为结点深度的线段树来维护这样一个过程。在遍历到某个点时，我们要加入所有以它为端点的路径；在 DFS 完某个点儿子时，我们要将儿子的 $f$ 数组合并到自己身上；在某个点从 DFS 栈中出去时，我们要删除所有 LCA 恰好为它的路径。也就是说，我们只需要支持单点更新，单点清除，以及合并。在修改 / 合并过程进行的同时，我们要进行答案的更新。注意红点的下方必须分叉，所以加入某个子树之前需要先更新答案。对于修改，我们用新加入的链和原来线段树中的点更新答案；在合并两棵树 $x, y$ 的时候，我们在合并之前用 $(\text{ls}(x), \text{rs}(y))$ 以及 $(\text{rs}(x), \text{ls}(y))$ 来更新答案即可。具体实现见代码。

第二部分

如果两条路径的 LCA 相同，那么它们的交一定过 LCA。

如上图，这两条路径的权值为 $\frac{两条链的总长度 + 蓝点距离 + 绿点距离 - 两条链的总费用 \times 2}{2}$。

我们首先假设所有链的 LCA 都是根结点。我们还是考虑枚举红点。对于某个蓝点，我们给它对应的绿点赋值为 $链长 - 费用 + 蓝点深度$。这样，对于某个红点下面的两个在不同子树内部的蓝点就可以用 $\frac{绿点权值和 + 绿点距离 - 红点深度 \times 2}{2}$ 来更新答案了。

这就相当于对于每个红点子树内的蓝点求绿点的最远点对。有一个性质是如果边权为正，那么两个集合的最远点对的端点一定是某个集合中最远点对的端点。于是我们合并最远点对即可。注意到红点下面还是需要分叉，处理的方法参考第一部分。

那么如果我们有多个 LCA 该怎么办呢？对每个 LCA 建虚树再跑上面的算法即可。

这样问题就得到了全面的解决，时间复杂度 $O(n \log n)$。

这道题目，无疑是善良的出题人无私的馈赠。不仅巧妙考察了选手二合一的思维能力，还对选手的手指速度有着极高的要求。无论是 NOI 测试还是平时练习，这都是一道一个顶俩的题目。出题人相信，这道美妙的题目，可以给拼搏于逐梦之路上的你，提供一个有力的援助。

代码实现

#include <bits/stdc++.h>