前言

以后的博客中可能会有一些计算几何的内容。

李超线段树已经在路上了。

~~又水了一篇博客呢~~

算法

本文主要参考这篇博客。

问题：给定一些形如 $y \le kx + b$ 的半平面，求它们的交。

不难发现这个图形的轮廓一定是某个上凸壳。

结论：将一条线视作一个点 $(k_i, b_i)$，做这些点的上凸壳，在凸壳上的点都在半平面交上。证明如下：

考虑怎么求半平面交。首先将斜率从大到小排序，然后将直线依次加入半平面交。发现半平面交一定满足：相邻两直线的交点横坐标单调递增。维护一个栈表示当前的半平面交，栈顶元素是其中斜率最小的。现在我们要加入一条斜率比栈中任何一个元素都小的直线。我们记新直线为 $l_1$，此时的栈顶为 $l_2$，栈顶下面的元素为 $l_3$。

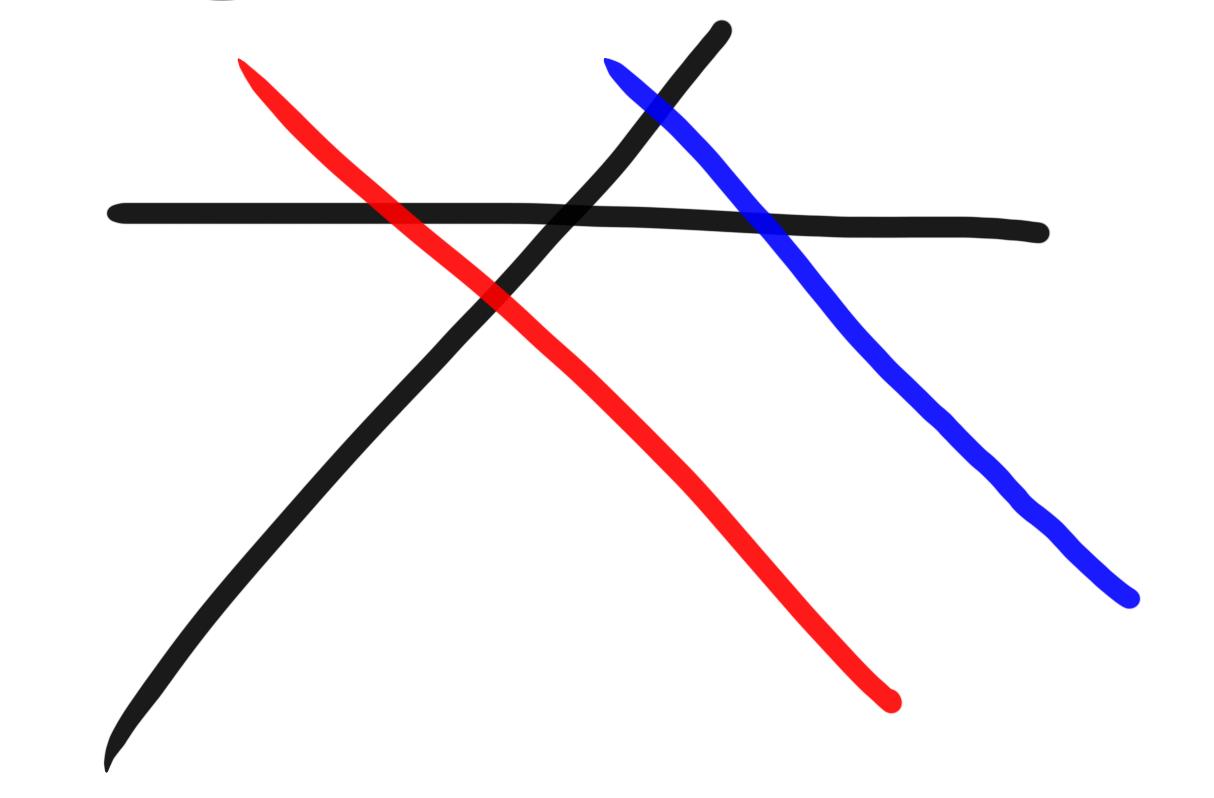
如图，如果 $l_1$ 和 $l_2$ 的交点在 $l_1, l_3$ 交点的右边（蓝色线），那么就直接把新的线加入栈中；否则（红色线），我们就需要弹出栈顶元素。也就是说，我们要一直弹栈，直到 $\frac{b_2 - b_1}{k_1 - k_2} > \frac{b_3 - b_1}{k_1 - k_3}$。

相信聪明的你已经已经看出，这个式子和凸包的式子十分类似。于是我们就可以用解凸包的方法来解半平面交了。

代码实现

这里放了一道 ZR 的题目，题意转化后就变成了给定 $n$ 条直线，每次询问编号在一个区间内部的直线中某个横坐标上的最小值。考虑建出线段树，然后每个节点维护一个多条直线的最小值的轮廓（其实就是半平面交）就行了。求半平面交的内容在结构体 ds 内部。时间复杂度 $O(n \log^2 n)$。（其实可以 $O(n \log n)$ 但是懒得写）

1	#include <bits/stdc++.h>
2	using namespace std;
3
4	namespace __main__ {
5	typedef long long ll;
6	typedef __int128 lll;
7	typedef double db;
8	const int maxn = 1e5, maxm = 1 << 18, logn = 17, maxk = maxn * 18, inf = 1e9;
9	const ll infl = ll(1e18 + .5);
10	int n, m, q, l_2[maxn + 3];
11
12	struct ds {
13	int n, a[maxn + 3], mn[logn + 3][maxn + 3], top, st[maxn + 3];
14	int tot, lft[maxm + 3], cnt[maxm + 3], id[maxk + 3];
15	ll b[maxn + 3], s[maxn + 3], p[maxk + 3];
16	pair<int, ll> pr[maxn + 3];
17
18	#define mid ((l + r) >> 1)
19	#define ls (x << 1)
20	#define rs (ls \| 1)
21
22	bool check(int i, int j, int k) {
23	return (lll) (b[i] - b[j]) * (a[i] - a[k]) < (lll) (b[i] - b[k]) * (a[i] - a[j]);
24	}
25
26	void bao(int l, int r) {
27	top = 0;
28	for (int i = l, id; i <= r; i++) {
29	id = pr[i].second;
30	while (top > 1 && !check(id, st[top], st[top - 1])) {
31	top--;
32	}
33	st[++top] = id;
34	}
35	}
36
37	void build(int x, int l, int r) {
38	if (l == r) {
39	pr[l] = make_pair(-a[l], l);
40	} else {
41	build(ls, l, mid);
42	build(rs, mid + 1, r);
43	inplace_merge(pr + l, pr + mid + 1, pr + r + 1);
44	}
45	bao(l, r);
46	cnt[x] = top, lft[x] = tot + 1;
47	for (int i = 1; i <= top; i++) {
48	id[++tot] = st[i];
49	if (i < top) {
50	db t = -1. * (b[st[i + 1]] - b[st[i]]) / (a[st[i + 1]] - a[st[i]]);
51	p[tot] = t - 3;
52	while (p[tot] * a[st[i]] + b[st[i]] <= p[tot] * a[st[i + 1]] + b[st[i + 1]]) {
53	p[tot]++;
54	}
55	p[tot]--;
56	}
57	}
58	p[tot] = infl;
59	}
60
61	ll query(int x, int l, int r, int lx, int rx, int k) {
62	if (l >= lx && r <= rx) {
63	int t = lower_bound(p + lft[x], p + lft[x] + cnt[x], k) - p;
64	return 1ll * k * a[id[t]] + b[id[t]];
65	}
66	ll ans = infl;
67	if (lx <= mid) {
68	ans = min(ans, query(ls, l, mid, lx, rx, k));
69	}
70	if (rx > mid) {
71	ans = min(ans, query(rs, mid + 1, r, lx, rx, k));
72	}
73	return ans;
74	}
75
76	#undef mid
77	#undef ls
78	#undef rs
79
80	void init() {
81	for (int i = 1; i <= n; i++) {
82	b[i] = 2ll * i * a[i] - 2 * s[i - 1];
83	s[i] = s[i - 1] + a[i];
84	mn[0][i] = a[i];
85	}
86	for (int k = 1; 1 << k <= n; k++) {
87	for (int i = 1, j = (1 << (k - 1)) + 1; i <= n - (1 << k) + 1; i++, j++) {
88	mn[k][i] = min(mn[k - 1][i], mn[k - 1][j]);
89	}
90	}
91	build(1, 1, n);
92	}
93
94	ll sum(int l, int r) {
95	return s[r] - s[l - 1];
96	}
97
98	int rmq(int l, int r) {
99	if (l > r) return inf;
100	int x = l_2[r - l + 1];
101	return min(mn[x][l], mn[x][r - (1 << x) + 1]);
102	}
103
104	ll solve(int x, int y) {
105	return query(1, 1, n, max(1 , x - y / 2), max(1, x - 1), y - 2 * x) + 2 * s[x - 1];
106	}
107	} a, b, c, d;
108
109	void main() {
110	scanf("%d %d %d", &n, &m, &q);
111	a.n = n - 1, c.n = n - 1;
112	b.n = m - 1, d.n = m - 1;
113	for (int i = 2; i <= max(n, m); i++) {
114	l_2[i] = l_2[i >> 1] + 1;
115	}
116	for (int i = 1, x; i < n; i++) {
117	scanf("%d", &x);
118	a.a[i] = x, c.a[n - i] = x;
119	}
120	for (int i = 1, x; i < m; i++) {
121	scanf("%d", &x);
122	b.a[i] = x, d.a[m - i] = x;
123	}
124	a.init(), b.init();
125	c.init(), d.init();
126
127	for (int i = 1, x_1, y_1, x_2, y_2, d_a, d_b, x; i <= q; i++) {
128	scanf("%d %d %d %d", &x_1, &y_1, &x_2, &y_2);
129	if (x_1 > x_2) swap(x_1, x_2);
130	if (y_1 > y_2) swap(y_1, y_2);
131	d_a = x_2 - x_1, d_b = y_2 - y_1;
132	x_2--, y_2--;
133	ll ans = a.sum(x_1, x_2) + b.sum(y_1, y_2);
134	if (d_a < d_b) {
135	x = d_b - d_a;
136	if (x & 1) x--;
137	ans += min(1ll * a.rmq(x_1, x_2) * x, min(a.solve(x_1, x), c.solve(n - x_2, x)));
138	} else {
139	x = d_a - d_b;
140	if (x & 1) x--;
141	ans += min(1ll * b.rmq(y_1, y_2) * x, min(b.solve(y_1, x), d.solve(m - y_2, x)));
142	}
143	printf("%lld\n", ans);
144	}
145	}
146	}
147
148	int main() {
149	__main__::main();
150	return 0;
151	}