题目大意
给定两个字符串 $S, T$(只包含 $4$ 个字母)和非负整数 $k$,定义模式串和文本串的一段是模糊匹配的,当且仅当对于模式串中的每个位置 $i$,都能在文本串中找到字符 $S_j = T_i$ 且 $\vert i - j \vert \le k$。
问模式串被匹配了几次。
我们记 $n = \vert S \vert, m = \vert T \vert$。
数据范围:$n, m, k \le 2 \times 10^5$。
$k = 1$ 时的样例: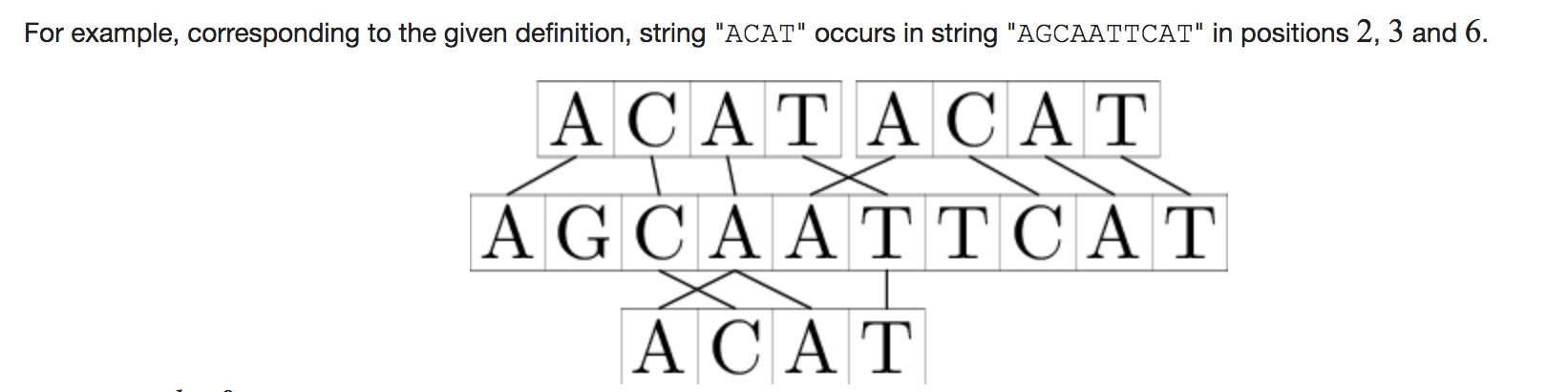
思路分析
由于字符集很小,我们考虑对于每种字符计算它能在那些位置出现。这显然可以通过差分 + 前缀和在线性时间内解决。
我们将字符 $ch$ 的可出现位置集合看作一个 01 串 $A(ch)$,那么答案就等于对于每个 $1 \le i \le m$,$A(T_i)$ 左移 $m - i$ 位后得到的 $m$ 个 01 串的交的大小。
于是我们可以对模式串中每个不同的字母构造多项式 $B_{ch}$,和 $A_{ch}$ 相乘后的多项式中,某项系数对应的位置合法当且仅当它的系数等于 $T$ 中 $ch$ 出现的次数。所以计算完这些我们最后就只需计算 $4$ 个 01 串的交。
时间复杂度瓶颈在于卷积,用 FFT 可以优化到 $O(n \log n)$。
代码实现
1 | |
2 | |
3 | |
4 | using namespace std; |
5 | |
6 | typedef double db; |
7 | const int maxn = 2e5, maxm = 1 << 19; |
8 | const db pi = acos(-1); |
9 | int n, m, L, M[200], a[5][maxn + 3], b[5][maxn + 3], c[5][maxn + 3], k, rev[maxm + 3]; |
10 | char s[maxn + 3]; |
11 | |
12 | struct complex { |
13 | db r, i; |
14 | complex(db r = 0, db i = 0): r(r), i(i) {} |
15 | friend complex operator+ (const complex &a, const complex &b) { |
16 | return complex(a.r + b.r, a.i + b.i); |
17 | } |
18 | friend complex operator- (const complex &a, const complex &b) { |
19 | return complex(a.r - b.r, a.i - b.i); |
20 | } |
21 | friend complex operator* (const complex &a, const complex &b) { |
22 | return complex(a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r); |
23 | } |
24 | friend complex operator/ (const complex &a, const db &b) { |
25 | return complex(a.r / b, a.i / b); |
26 | } |
27 | }; |
28 | |
29 | complex A[maxm + 3], B[maxm + 3], C[maxm + 3]; |
30 | |
31 | void dft(complex a[], int n, int type) { |
32 | for (int i = 0; i < n; i++) if (i < rev[i]) { |
33 | swap(a[i], a[rev[i]]); |
34 | } |
35 | for (int k = 1; k < n; k *= 2) { |
36 | complex x = complex(cos(pi / k), type * sin(pi / k)); |
37 | for (int i = 0; i < n; i += k * 2) { |
38 | complex y = 1; |
39 | for (int j = i; j < i + k; j++, y = x * y) { |
40 | complex p = a[j], q = a[j + k] * y; |
41 | a[j] = p + q, a[j + k] = p - q; |
42 | } |
43 | } |
44 | } |
45 | if (type == -1) { |
46 | for (int i = 0; i < n; i++) { |
47 | a[i] = a[i] / n; |
48 | } |
49 | } |
50 | } |
51 | |
52 | inline int id(char ch) { |
53 | return M[ch]; |
54 | } |
55 | |
56 | int main() { |
57 | M['A'] = 0, M['T'] = 1, M['G'] = 2, M['C'] = 3; |
58 | scanf("%d %d %d %s", &n, &m, &L, s + 1); |
59 | for (int i = 1; i <= n; i++) { |
60 | int x = id(s[i]), l = max(1, i - L), r = min(n, i + L); |
61 | a[x][l - 1]++, a[x][r]--; |
62 | } |
63 | for (int k = 0; k < 4; k++) { |
64 | for (int i = 1; i < n; i++) { |
65 | a[k][i] += a[k][i - 1]; |
66 | } |
67 | for (int i = 0; i < n; i++) { |
68 | a[k][i] = a[k][i] > 0; |
69 | } |
70 | } |
71 | scanf("%s", s + 1); |
72 | for (int i = 1; i <= m; i++) { |
73 | b[id(s[i])][m - i] = 1; |
74 | } |
75 | for (k = 0; 1 << k <= n + m - 2; k++); |
76 | for (int i = 1; i < 1 << k; i++) { |
77 | rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (k - 1)); |
78 | } |
79 | for (int t = 0; t < 4; t++) { |
80 | int sum = 0; |
81 | for (int i = 0; i <= n - 1; i++) { |
82 | A[i] = a[t][i]; |
83 | } |
84 | for (int i = n; i < 1 << k; i++) { |
85 | A[i] = 0; |
86 | } |
87 | for (int i = 0; i <= m - 1; i++) { |
88 | B[i] = b[t][i], sum += b[t][i]; |
89 | } |
90 | for (int i = m; i < 1 << k; i++) { |
91 | B[i] = 0; |
92 | } |
93 | dft(A, 1 << k, 1), dft(B, 1 << k, 1); |
94 | for (int i = 0; i < 1 << k; i++) { |
95 | C[i] = A[i] * B[i]; |
96 | } |
97 | dft(C, 1 << k, -1); |
98 | for (int i = m - 1; i < n; i++) { |
99 | int x = C[i].r + .5; |
100 | if (x == sum) { |
101 | c[t][i + 1] = 1; |
102 | } |
103 | } |
104 | } |
105 | int ans = 0; |
106 | for (int i = m; i <= n; i++) { |
107 | if (c[0][i] && c[1][i] && c[2][i] && c[3][i]) { |
108 | ans++; |
109 | } |
110 | } |
111 | printf("%d\n", ans); |
112 | return 0; |
113 | } |