「Codechef SKIRES」Ski Resort（最小割）

题目大意

「Codechef SKIRES」Ski Resort

给定 $n \times m$ 的网格图，每个格子有一个高度 $h_{i, j}$。给一个格子的高度增加 $x$ 需要花费 $x$ 的代价。你要调整某些格子的高度，使得不存在高度单调不下降的，从起点到终点的路径。求需要花费的最小代价。

数据范围：$n, m \le 50$。

思路分析

看到 “不存在……的路径” 就想到最小割建图。但是直接对于每对相邻的格子建图不可行，因为一个格子高度的增加可能同时影响到与之相邻的几个格子。也就是说，如果需要使格子 $x$ 的高度比格子 $y_1, y_2, \cdots, y_k$ 大，所需要的代价不是 $\sum_{i = 1}^{k} \text{cost}(x, y_i)$，而是 $\max_{i = 1}^{k} \text{cost}(x, y_i)$，其中 $\text{cost}(x, y)$ 表示格子 $x$ 要比格子 $y$ 高需要花费的代价，也就是 $\max{0, h(y) - h(x) + 1}$。

所以，我们对于每个格子拆点，一起考虑它周围一圈的格子。例如对于下图中的格子：

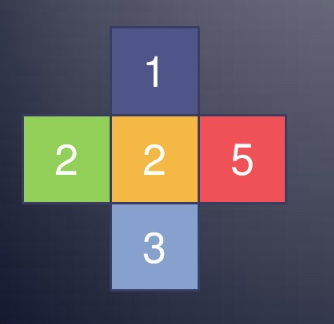
需要建如下结构的图：

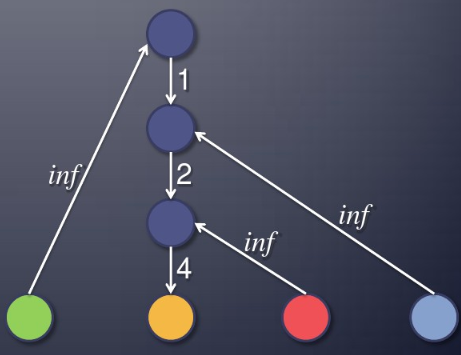
另外注意一些小细节：

• $-1$ 最好提前判掉，否则可能会引起不必要的麻烦。
• 起点和终点的建图需要特判，因为题意要求起点和终点的高度不能变化。

代码实现

本菜鸡的 Dinic 跑不过（明明各种优化都加满了啊 QAQ），所以使用了 ISAP 来实现最大流。

#pragma GCC optimize(2)